The Timeform Knowledge: Each-Way and Place Betting

Few subjects can be much more confusing for the newcomer to horseracing and betting than that of each-way betting. To this day, misconceptions abound even among those who have bet on the sport for many years.

That probably does not include many of those of you who are currently reading this piece: if you got beyond the modules which mentioned Monte-Carlo simulation and the Kelly Criterion, I am guessing each-way betting will not be much of a mystery to you!

Nonetheless, it is worth stating clearly at the outset what the conditions of each-way betting involve.

An each-way bet is a bet on a horse to win and to place, with the number of places offered being determined by the number of runners and the type of race, while the return for a successful place part of the bet is derived from a fixed fraction of the win odds of the horse in question.

An each-way bet is, therefore, two bets in one. If you state, say, £10 each way, the bet will cost you £20 (£10 as a win bet, and £10 as a place bet).

The reason why you cannot bet on a horse just to place – other than in separate place-only markets – is also the reason why each-way betting is so attractive in some circumstances (and unattractive in others). As place returns are derived from win odds according to fixed rules, there are times when they become very advantageous to punters. 

Those rules are as follows:

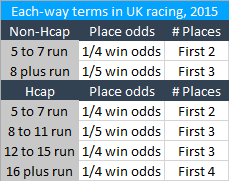
So, if you back a horse at 8/1 you would be paid 2/1 for the place part of the bet (8/(1*4)) if the race is a handicap, other than an 8-runner to 11-runner one, or if it is a non-handicap of 5 to 7 runners; otherwise, you would be paid 1.6/1 (8/(1*5)). Races with fewer than 5 runners pay one place (i.e. the win) only. 

Such fixed rules, in which place odds are crudely derived from win odds, are likely to lead to anomalies, especially at the points at which you move from one category to the next.

Regular readers will recall that the % chance assigned to a horse in the win market is deduced from 100/((A/B)+1), where A and B are the numerator and denominator of the fractional odds, so that, say, a horse with odds of 5/2 has a % chance of 100/(2.5+1) = 28.6%.

When you sum this for all horses in a race you get the % for the race itself, which will (other than in exceptional circumstances) be greater than 100, for that is how bookmakers seek to ensure themselves a profit.

The same exercise can be done for the place part of an each-way bet, then divided by the number of places being paid to get a % per-place for the race also.

If you did this for every race over jumps in Britain in 2014 you would find circumstances in which the place book was less than 100% (known as “over-broke”) on average across what were many instances. Specifically, these were for: 8-runner non-handicaps (99.9% per-place on average) and 16-, 17- and 18-runner handicaps (collectively 98.0% per-place on average). If allowed to back place-only, you could (at least in theory) guarantee a profit whatever the outcome.

But, you will recall, you cannot back place-only (for this very reason!) and must also back any horse(s) in question for a win.

A better indication of the theoretical value of an each-way bet is therefore to consider the race % for the win part of the bet combined with the race % for the place part of the bet (with the latter being the % PER-PLACE).

This gives less exciting findings – the golden goose of a theoretically guaranteed profit has suddenly flown off! – but does again identify certain types of races which are better than others.

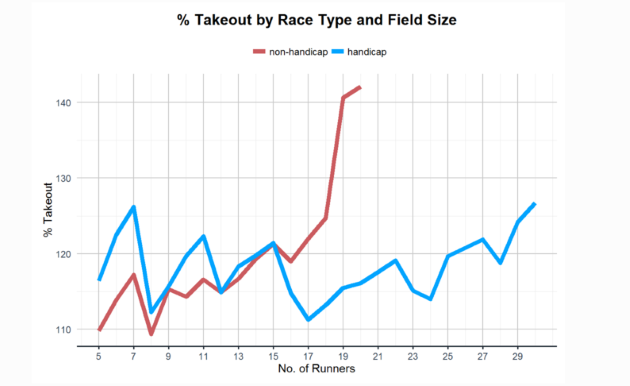
The lower the point on the graph, the better, for that means the theoretical edge to the bookmaker is smaller. It can be seen that 8-runner races (handicaps and non-handicaps) are good, as are 12-runner handicaps (if less so) and 16-runner and 17-runner handicaps.

Each one of those scenarios comes at, or just after, a shift from one each-way category to the next.

Those figures are averages across a large number of races for the entirety of a year of jumps racing in Britain, and there will be instances that are more or less favourable than that average.

In particular, things get much more interesting when the market in question is lop-sided. In such cases, each-way betting can become very attractive indeed.

The possible illustrations here are well-nigh infinite, so a couple of extreme examples have been chosen.

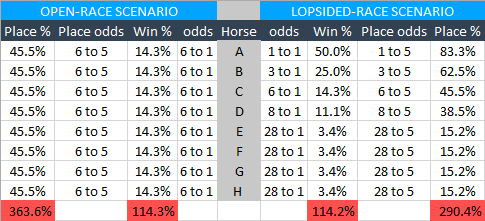
Both races have 8 runners and almost exactly the same race win %, but the one on the left is remarkably open (every horse is at the same price of 6/1) while the one on the right is lop-sided, with one strong contender, three other realistic ones and four rank outsiders.

The effect on the place part of the bet is major. The “open” race comes in at 121.2% per place (there are three places), and 117.8% for an each-way bet (the win % and the per-place % averaged); but the “lop-sided” race comes in at 96.8% per place, and 105.5% for an each-way bet.

The latter proposition is considerably more attractive than the former, all other things being equal, and you still have not considered extraneous factors, such as that a horse under consideration may have a much better chance than as represented by a crude derivation from its win odds. 

Such considerations may be strong enough to over-rule the mathematics on occasions, but each-way punters could do a lot worse than concentrating on those instances in which the balance is tipped in their favour.

There is no higher recommendation for this than that your bookmaker may well not be especially keen on your custom if you adopt such an approach!