Place Terms and When to Back Each-Way
 Betting expert Simon Rowlands explains the maths behind each-way betting advantage, and how to play smarter by using place terms in your favour.
Betting expert Simon Rowlands explains the maths behind each-way betting advantage, and how to play smarter by using place terms in your favour.
There can be few aspects of betting that are more misunderstood than each-way. Some could not do without it, while others are dismissive of it, seeing it as an admission of betting weakness.
The latter group may have a point when yet another media pundit states “this is an each-way price” or puts a horse up as an “each-way selection” seemingly without thinking. The inference may be that they do not really fancy the horse to win and that an each-way recommendation is a fudge.
Maybe. However, there are circumstances in which each-way betting is eminently sensible, including to do with the nature of the horse or the race itself, and there are times when it makes perfect mathematical sense.
How place terms work
A reminder that an each-way bet is effectively two bets in one: a bet to win, and a bet to place, with the odds for the latter derived directly from the odds of the former. The standard place terms are as follows:
· Handicaps of 16 or more runners: 1/4 win odds on first four places
· Handicaps of 12 to 15 runners: 1/4 win odds on first three places
· All other races of 8 or more runners: 1/5 win odds on first three places
· All races of 5 to 7 runners: 1/4 win odds on first two places
· All races of fewer than 5 runners: win only
Regular readers will be familiar with the maths involved with calculating the theoretical edge – or “over-round” – involved in a win market, and the same can be applied to the place odds derived directly from those win odds.
The calculation is to sum the percentages arising from dividing each horse’s fractional odds, plus one, into 100 (if working with decimal odds, such as on an Exchange, the “plus one” is not required). So, a horse that is 4/1 becomes 100/(4+1) = 20%.
If you add these percentages together for all horses in a race they are likely to come to a bit over 100 – in the 110 to 120 range for most races – and represent the total amount you would have to stake in proportion to each horse’s odds to guarantee a return of 100 regardless of the result.
The same can be done for the place market derived directly from those win odds, so that in a 10-runner race in which a horse is 10/1, the place odds become 2/1 (10 divided by 5) and the place percentage is 100/(2+1) = 33%.
You then divide the sum of these percentages for all runners in a race by the number of places on offer in that race to get the per-place percentage, such as 330%/3 = 110% per-place.
When each-way betting makes more sense
The great thing about the place part of an each-way bet is that such fixed rules for deriving place odds from win odds throw up opportunities in which place betting is mathematically advantageous to the punter even when win betting is not.
This particularly occurs at the boundary between categories, which is why you will find each-way veterans cooing over “dead-eight" races (races with exactly eight runners, especially those in which the betting is lop-sided) and salivating over 16-runner handicaps.
It is also the reason why place-only betting is not allowed, unless it is in a dedicated place market. Otherwise, it would sometimes be possible to back every outcome to guarantee a profit. But it does mean that an each-way bet, in which a win bet is “sweetened” by the place element, may be more appealing (all other things being equal) than a win bet.
When does this occur? Well, it depends. If you really want to answer this question then the best thing to do is to create a spreadsheet which works out the win % and the per-place % for the race in question. The each-way over-round will be the average of those two.
Both will depend not only on the type of race and number of places on offer but the distribution of odds, such as whether or not they are being skewed by a short-priced favourite.
As a guide, though, we can look at the reality of what actually occurs, such as in all Flat races in Britain in 2018. The following table shows the average win % and per-place % separately for non-handicaps and handicaps with different numbers of runners:
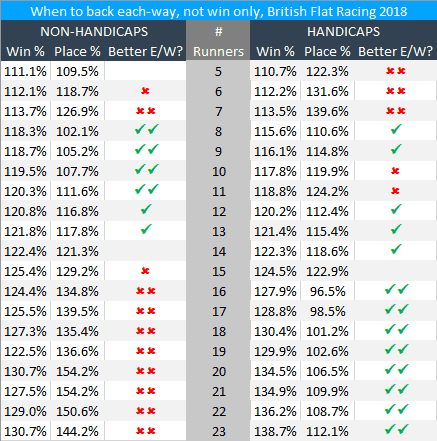
It can be seen that there are “sweet spots” of 8 to 11 runners in non-handicaps and 16 runners plus in handicaps. By contrast, it is seldom a good policy to back each-way rather than win only in 16-plus non-handicaps or in 5- to 7-runner handicaps.
However, it should be remembered that an each-way bet is a win bet plus a place bet, so bad value with the former may more than offset better value with the latter.
The table identifies when each-way has been a better proposition mathematically than a win only bet, but the each-way over-round is an average of that win % and that per-place %.
In 2018 Flat races in Britain this came in at less than 115% in only: 5-runner non-handicaps; 8- to 10-runner non-handicaps; 8-runner handicaps; and 16- and 17-runner handicaps. Those are the races to concentrate on for each-way purposes, all other things being equal.
What about enhanced place terms?
Those standard place terms mentioned earlier are the starting point for each-way betting, but bookmakers will sometimes try to tempt you in with variations, especially by offering additional places.
The best way to calculate the value, or otherwise, of such a proposition is to run it through that spreadsheet. Besides anything else, The Good Lord (bookmakers) may be inclined to giveth (in enhanced place terms) as well as taketh away (with stingier win odds).
Some of the enticements are a bit easier to figure out than others. For instance, offering 1/4 the odds first 3 places instead of 1/5 odds for the same enhances the place odds on a 10/1 shot from 2/1 (33%) to 5/2 (28%).
Others require a bit more calculation. But, as examples, these popular enhancements – some of which were in evidence at last week’s Cheltenham Festival – play out as follows:
1/4 odds first 4 à 1/5 odds first 5, improved place odds by 6.6% per-place on average
1/4 odds first 3 à 1/5 odds first 4, improved place odds by 15.9% per-place on average
1/4 odds first 2 à 1/5 odds first 3, improved place odds by 33.6% per-place on average
In summary, obtaining an extra place for a slight reduction in place odds is very likely to be worth it in mathematical terms. Just keep an eye on whether you are giving up more in the win part of an each-way bet than you are gaining in the place part.
The maths behind betting each-way
That is at the race-level, but things get more difficult when considering whether or not to back an individual horse at, say, 12/1 1/4 odds first four places or 10/1 1/5 odds first five places.
My best attempt at solving this particular conundrum (after I had corresponded with a senior trader at one of the big bookmakers) is as follows:
If we assume, for convenience, that 12/1 in the first instance are fair odds for the horse to succeed in a 100% book, then the implied win book in the second case becomes: (100*13)/11 = 118.2%.
If we also assume, likewise for convenience, that 1/4 of 12/1 (that is, 3/1) are fair odds for a place when four places are on offer, then the implied place book in the second instance becomes: (400*33.3)/(5*25) = 106.6%.
And an each-way bet coming out at 100% win-and-place combined in the first instance becomes 111.9% in the second, so the first bet (12/1, 1/4 odds for four places) is superior to the second.
The calculation for the second proposition where we assume that the first proposition is fair, is:
((100*A)/B)+((100*C*D)/(E*F)), all divided by two
where “A” is the win odds plus one in the first case; “B” is the win odds plus one in the second case; “C” is the number of places in the first case; “D” is the place odds plus one divided into 100 in the second case; “E” is the number of places on offer in the second case; and “F” is the place odds plus one divided into 100 in the first case.
There are some real-life complicating factors which you may wish to insert, such as that a race of this nature might have, say, a 120% win book (so change the first 100 in the equation to 120) but a 100% per-place book (so leave the second 100), in which case the former has a slightly bigger influence.
But, if you want a rule of thumb in this area, it is that 1/5 odds for an extra place is better than 1/4 odds for four places when the win odds are the same, but that even a small reduction in win odds (such as from 8/1 to 15/2) nullifies that edge.
Each-way betting is a complicated matter in mathematical terms – I think you will agree! – even before you get onto the suitability of individual horses (and jockeys) for win or each-way purposes. A few rules of thumb could be considered preferable to a lifetime of slaving over spreadsheets.















